| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- leetcode
- leetcode 238
- leetcode 234
- leetcode 5
- Hortonworks Sandbox
- 문자열 조작
- leetcode 819
- Python
- docker로 airflow 설치하기
- leetcode125
- leetcode 15
- 올바른 변수명 짓기
- 머신러닝
- 빅데이터를 지탱하는 기술
- wargame.kr
- leetcode 344
- 블로그 이전했어요
- leetcode 937
- 배열
- leetcode 121
- ctf-d
- leetcode 49
- 데이터레이크와 데이터웨어하우스
- webcrawler
- Hadoop
- leetcode 561
- 컴퓨터구조
- MapReduce 실습
- airflow docker
- 스파크 완벽 가이드
- Today
- Total
HyeM
[Do it] 로지스틱 회귀, 시그모이드 함수, 로지스틱 손실 함수 본문
04-1 | 초기 인공지능 알고리즘과 로지스틱 회귀를 알아봅니다 .
#1. 퍼셉트론

1957년 이진 분류 문제에서 최적의 가중치를 학습하는 퍼셉트론 알고리즘 발표
* 이진 분류 : 임의의 샘플 데이터를 True나 False로 구분하는 문제
직선 방정식을 사용해 선형 회귀와 유사한 구조를 띈다.
하지만 마지막 단계에서 샘플을 이진 분류하기 위해 계단 함수를 사용하고, 계단 함수를 통과한 값을 다시 가중치와 절편으로 업데이트(학습)하는데 사용함. 계단함수는 x가 0보다 크거나 같으면 1로, 0보다 작으면 -1로 분류한다,
즉, 퍼셉트론은 선형함수를 통과한 값 z를 계단 함수로 보내 0보다 큰지 작은지 검사하여 1과 -1로 분류하는 아주 간단한 알고리즘이다.

만약 여러개의 특성 n개를 사용한다면, 선형함수를 다음과 같이 표기할 수 있다.
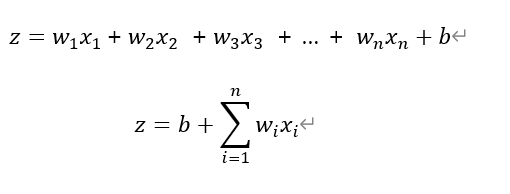
퍼셉트론은 사이킷런 패키지에서 Perceptron이라는 이름으로 클래스를 제공한다.
#2. 아달린

1960년에 퍼셉트론을 개선한 적응형 선형 뉴런인 아달린을 발표
역방향 계산이 계단 함수 출력이후에 일어나지 않고 선형 함수 출력 이후에 진행된다.
(나머지 요소는 퍼셉트론과 동일)
#3. 로지스틱 회귀
로지스틱 회귀는 아딜린에서 조금 더 발전한 형태이다.

로지스틱 회귀는 선형함수를 통과하여 얻은 Z를 임계함수에 보내기 전에, 활성화 함수를 거쳐 변형시키고, 통과한 값이 a가 된다. 마지막 단계에서 임계 함수를 사용하여 예측을 수행한다.
임계함수는 아달린이나 퍼셉트론의 계단 함수와 역할은 비슷하지만 활성화 함수의 출력을 사용한다는 점이 다르다.
활성화 함수는 비선형 함수를 사용한다. 그 이유는 만약 선형함수라면, 임계 함수 앞에서 뉴런을 여러개 쌓아도 결국 선형 함수가 되기 때문에 비선형 함수를 사용한다. 로지스틱 회귀의 활성화 함수는 '시그모이드 함수'이다.
04-2 | 시그모이드 함수로 확률을 만듭니다
활성화 함수인 시그모이드 함수는 0~1사이의 확률값으로 변환해주는 역할을 한다.
시그모이드 함수 만드는 과정에 오즈비와 로짓함수 개념이 들어가는데, 오즈비는 성공 확률과 실패 활귝의 비율을 나타내는 통계이고, 로짓 함수는 p가 0.5일때 0이 되고, p가 0과 1일때 각각 무한대로 음수와 양수가 되는 특징을 가진다.

로짓 함수를 그래프로 나타내면, 새로축은 z를, 가로축은 p가 되는데, 이를 z에 대한 식으로 바꾸면 로지스틱 함수가 된다.
그래프로는 S자 형태를 띄게 된다.

정리를 해보면, 로지스틱 회귀는 이진 분류가 목표이므로 -∞ 부터 +∞의 범위를 가지는 z의 값의 값을 조절할 필요가 있다. 이를 위해서 시그모이드 함수를 두어 통과하면 z를 확률처럼 해석할 수 있다. 그리고 시그모이드 함수의 확률인 a를 0과 1로 구분하기 위해서 마지막에 임계함수를 사용했다. 그 결과 입력 데이터x는 0 또는 1의 값으로 나누어진다.
04-3 | 로지스틱 손실 함수를 경사 하강법에 적용합니다
로지스틱 회귀와 같은 분류는 분류의 비율을 높이기 위해서, 경사 하강법의 손실 함수를 사용할 수 없어, 로지스틱 손실 함수를 사용한다.
로지스틱 손실 함수는 다중 분류를 위한 손실 함수인 '크로스 엔트로피 손실 함수'를 이진 분류 버전으로 만든 것이다.

a는 활성화 함수가 출력한 값이고, y는 타깃이다. 타깃은 그렇다, 아니다의 1과 0으로 나뉘니, 아래와 같이 식이 나뉜다.

이때, 두 식의 값을 최소로 만들면 a값이 우리가 원하는 목표치가 되게 된다. 만약 양성클래스인 경우 로지스틱 손실 함수의 값을 최소로 만들기 위해서 a는 1에 가까워지고, 반대로 음성 클래스인 경우엔 a가 0에 가까워진다.
이제 이 로지스틱 손실 함수를 미분하게 되면, 앞에서 본 제곱 오차의 미분과 크게 다르지 않음을 확인할 수 있다.

미분의 연쇄 법칙에 의하여 미분해보면, 제곱오차를 미분한 결과와 로지스틱 손실함수를 wi에 대해 미분한 결과가 일치함을 알 수 있다.

오른쪽부터 보면 로지스틱 손실 함수 L은 a에 대해 미분하고, a는 z에 대하여 미분하고, z는 w에 대해 미분한다.
그리고 각 도함수의 곱을 가중치 업데이트에 사용한다. 이렇게 미분이 연쇄법칙에 의해 진행되는 구조를 보고 '그레이디언트가 역전파된다'라고 말한다.
가중치 업데이트 방법은 로지스틱 손실 함수를 가중치에 대해 미분한 식을 가중치에서 빼면 된다.

절편 업데이트 방법 역시 로지스틱 손실 함수를 절편에 대해 미분한 식을 가중치에서 빼면 된다.

'Study > AI&DeepLearning' 카테고리의 다른 글
| [Do it] 검증세트와 전처리 과정, 과대적합과 과소적합 (0) | 2021.06.02 |
|---|---|
| [Do it] 로지스틱 뉴런 단일층 신경망 구현, 사이킷런 로지스틱 회귀 수행 (0) | 2021.05.05 |
| [Do it] 3-3|3-4_선형회귀, 경사하강법 (0) | 2021.04.05 |
| [Do it] 3-1|3-2_선형회귀, 경사하강법 (0) | 2021.03.29 |
| [Do it] 02-2_Numpy, Matplotlib (0) | 2021.03.29 |




